A Beginner Intro to Convolutional Neural Networks
explore Convolutional Neural Networks
Check out the lesson1 from Stanford Convolutional Neural networks for visual recognition class to know the History behind Neural Networks.
Check out Beginner intro to Neural Networks before you dig into CNN
What are Neural networks?
Neural networks are set of algorithms inspired by the functioning of human brian. Generally when you open your eyes, what you see is called data and is processed by the Nuerons(data processing cells) in your brain, and recognises what is around you. That’s how similar the Neural Networks works. They takes a large set of data, process the data(draws out the patterns from data), and outputs what it is.
What they do ?
Neural networks sometimes called as Artificial Neural networks(ANN’s), because they are not natural like neurons in your brain. They artifically mimic the nature and funtioning of Neural network. ANN’s are composed of a large number of highly interconnected processing elements (neurones) working in unison to solve specific problems.
ANNs, like people,like child, they even learn by example. An ANN is configured for a specific application, such as pattern recognition or data classification,Image recognition, voice recognition through a learning process.
Neural networks (NN) are universal function approximaters so that means neural networks can learn an approximation of any function f() such that.
y = f(x)
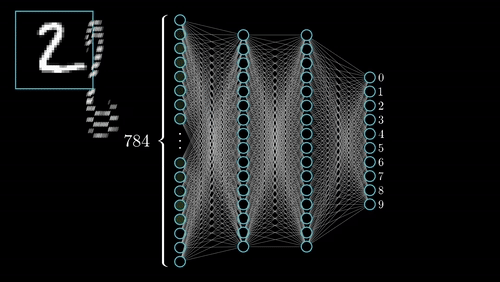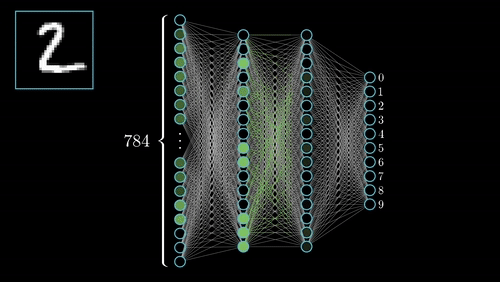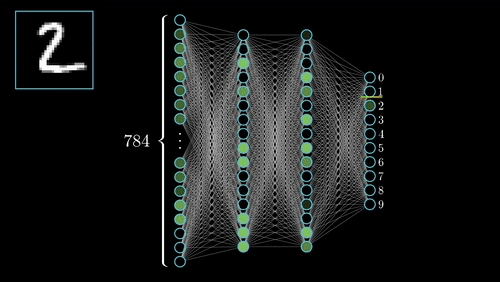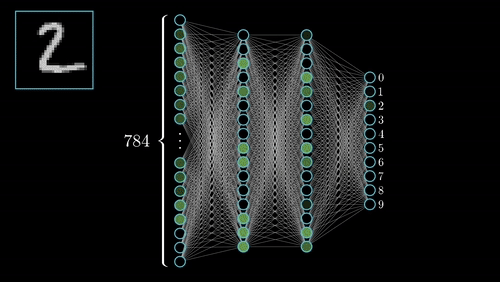
Neural networks has several other categories of Networks like Convolutional Neural Networks(CNN), Recurrent Neural Networks(RNN), Long Short Term Memory Networks(LSTM).
Why Convolutional Neural Networks?
We know that the Neural Networks are good at Image Recognition. Now if you consider this image recognition task , this can even be achieved by Neural networks, but the problem is , if the image is of Large pixels then the no.of.parameters for a Neural network increases. This makes Neural networks slow and consumes a lot of computational power.
for Ex: if you process a 64*64*3 size image, then you will get 12288 input parameters. but what if the image is a high resolution with 1000*1000*3, then it has 3million input parameters to process. This takes lot of time and computational power.
check out here for more on this.
Applications:
Object detection:
Edge detection:
Semantic segmentation:
Image caption:
Question &Answering:
Obeject tracking
Video classfication
style transfer
……….
What are Convolutional Neural Networks?
Unlike Neural Networks, Convolutional neural networks ingest and process images as tensors, and tensors are matrices of numbers with additional dimensions.
Computers see images differently than humans. they see images as pixels.
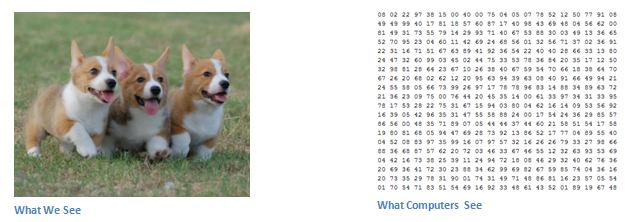
let’s say we have a color image in JPG form and its size is 480 x 480. The representative array will be 480 x 480 x 3(channels =RGB). Each of these numbers is given a value from 0 to 255 which describes the pixel intensity at that point. These numbers, while meaningless to us when we perform image classification, are the only inputs available to the computer.
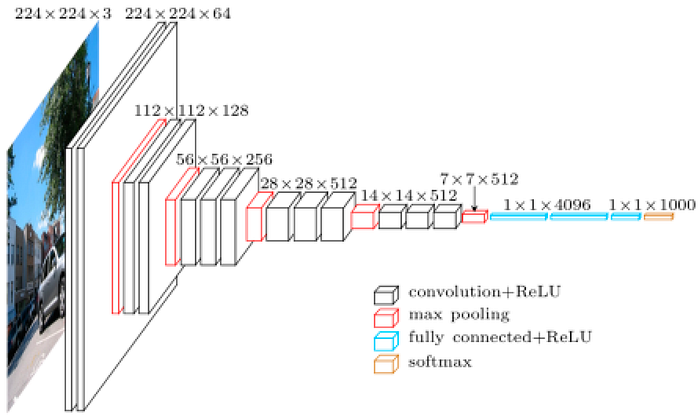
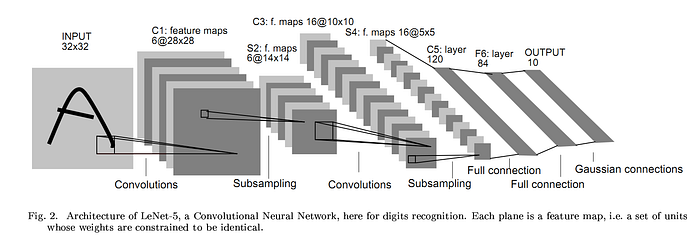
for more convNet images check here. you will get an idea how they looks.
Convolutional Neural Networks have 2 main components.
- Feature learning: you can see convolution, ReLU,Pooling layer phases here. Edges,shades,lines,curves, in this Feature learning step are get extracted.
- classification:you see Fully Connected(FC) layer in this phase. They will assign a probability for the object on the image being what the algorithm predicts it is.
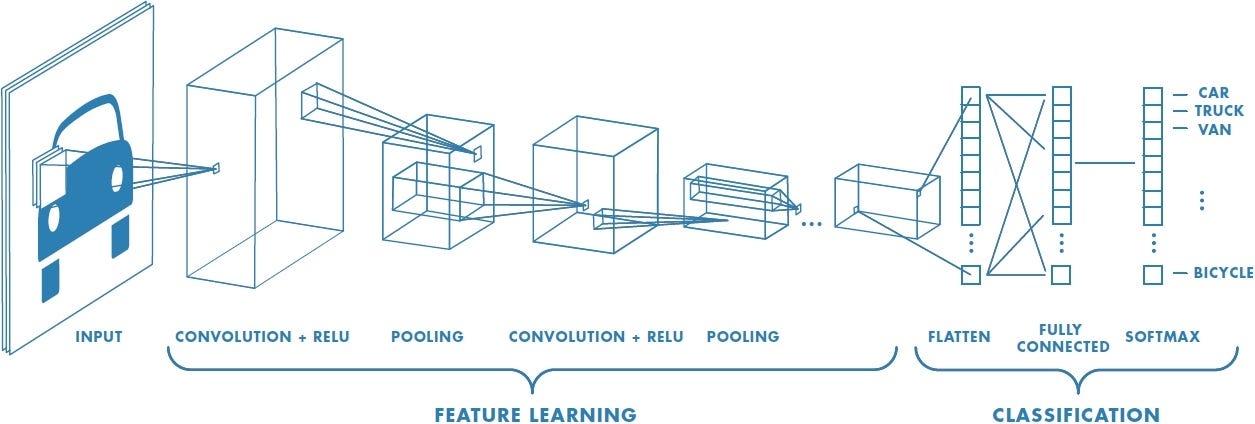
lets see Feature learning phase here.
Phase-1: Feature learning
Convolution :-
input image:
As we discussed above, every image can be considered as a matrix of pixel values. Consider a 5 x 5 image whose pixel values are only 0 and 1 (note that for a grayscale image, pixel values range from 0 to 255, the green matrix below is a special case where pixel values are only 0 and 1):
Filter:
This input image is multiplied by a filter to get the Convolved layer. these filter differs in shapes and in values to get different features like edges, curves, lines. this filter sometimes called as Kernel, Feature detector.
lets consider 3*3 filter to extract some features from the input image which is in pixel values at input image above.
Convolved layer:
each value in each pixel of input image is multiplied with respective value and pixel of filter that gives Convolved layer here. this Convlayer here sometimes called as Convolutional Feature, Feature map, Filter map here.
The result of Convolved feature depends on the three parameters. that we need to define before the convolution is performed.
- Depth: in the above input image we just considered image with depth =1, but most of the inputs will be of depth =3 which is of 3 channels like Red, Green, Blue.
- Stride: Stride is the number of pixels by which we slide our filter matrix over the input matrix. When the stride is 1 then we move the filters one pixel at a time. When the stride is 2, then the filters jump 2 pixels at a time as we slide them around. Having a larger stride will produce smaller feature maps.
- Padding: is like how many pixel you add extra to image. mostly padding would be 1. look at the fig below. image with 4*4 pixel padded with 1.

Summary. To summarize, the Conv Layer:
- Accepts a volume of size W1×H1×D1
- Requires four hyperparameters:
— Number of filters K,
— their filter size F,
— the stride S,
— the amount of zero padding P.
- Produces a volume of size W2×H2×D2 where:
— W2=(W1−F+2P)/S+1
— H2=(H1−F+2P)/S+1 (i.e. width and height are computed equally by symmetry)
— D2=K
ReLU(Rectified Linear Unit):introduces non-linearity
An additional operation called ReLU has been used after every Convolution operation. Relu is a non- linear operation
ReLU is an element wise operation (applied per pixel) and replaces all negative pixel values in the feature map by zero. The purpose of ReLU is to introduce non-linearity in our ConvNet, since most of the real-world data we would want our ConvNet to learn would be non-linear (Convolution is a linear operation — element wise matrix multiplication and addition, so we account for non-linearity by introducing a non-linear function like ReLU).
Pooling layer:
In this phase the dimensionality of convlayer or feature map gets reduced keeping the important information. sometimes this spatial pooling is also called Downsampling or subsampling. this pooling layers may be Max pooling, Avg pooling, sum pooling. mostly we see Max pooling is used most.
- Accepts a volume of size W1×H1×D1
- Requires two hyperparameters:
— their spatial extent F,
— the stride S,
- Produces a volume of size W2×H2×D2 where:
— W2=(W1−F)/S+1
— H2=(H1−F)/S+1
— D2=D1
Phase-2:Classification
Fully connected layer:

The Fully Connected layer is a traditional Multi Layer Perceptron that uses a softmax activation function in the output layer . The term “Fully Connected” implies that every neuron in the previous layer is connected to every neuron on the next layer.
The output from the convolutional and pooling layers represent high-level features of the input image. The purpose of the Fully Connected layer is to use these features for classifying the input image into various classes based on the training dataset.
The sum of output probabilities from the Fully Connected Layer is 1. This is ensured by using the Softmax as the activation function in the output layer of the Fully Connected Layer. The Softmax function takes a vector of arbitrary real-valued scores and squashes it to a vector of values between zero and one that sum to one.
In the above figure using softmax to the fully connected layer gives the probability values of classes like car, truck, and bicycle.
I suggest you to check this blog here with excellent paper explanations
Reference:
To Explore more check out the “complete chart of Neural Networks”.
Stanford tutorial on ConvNets here.
ujjwalkarn blog here.
skymind blog here.
Thank you so much for being here.
comment down your views, if any mistakes found the blog will be updated with effect.
